【译】 CUTLASS：CUDA C++ 中的快速线性代数

Posted Mar 9, 2024

By Andrew Kerr 40 min read

原文：CUTLASS: Fast Linear Algebra in CUDA C++

2018 年 5 月 21 日更新：CUTLASS 1.0 现已作为开源软件在 CUTLASS 存储库中提供。CUTLASS 1.0 已从我们在以下博客文章中描述的预览版本中发生了重大变化。我们已将 GEMM 计算的结构分解为更深层次的结构化基元，用于加载数据、计算谓词掩码、在 GEMM 层次的每个级别流式传输数据以及更新输出矩阵。CUTLASS 1.0 在 Doxygen 文档和我们在 2018 年 GPU 技术大会上的演讲中进行了描述。

矩阵乘法是许多科学应用中的关键计算，尤其是在深度学习中。现代深度神经网络中的许多操作要么被定义为矩阵乘法，要么可以被转化为矩阵乘法。

例如，NVIDIA cuDNN 库使用各种矩阵乘法形式实现神经网络的卷积，例如将直接卷积的经典公式作为图像到列和滤波器数据集之间的矩阵乘积¹。矩阵乘法也是基于快速傅里叶变换 (FFT)² 或 Winograd 方法³ 计算卷积时的核心例程。

在构建 cuDNN 时，我们从 cuBLAS 库中通用矩阵乘法 (GEMM) 的高性能实现开始，对其进行补充和定制，以高效计算卷积。如今，我们调整这些 GEMM 策略和算法的能力对于为深度学习中的许多不同问题和应用程序提供最佳性能至关重要。

借助 CUTLASS，我们希望为每个人提供他们使用高性能 GEMM 构造作为构建块在 CUDA C++ 中开发新算法所需的技术和结构。密集线性代数的灵活高效应用在深度学习和更广泛的 GPU 计算生态系统中至关重要。

介绍 CUTLASS

今天，我们介绍了 CUTLASS（用于线性代数子例程的 CUDA 模板）的预览版，它是一组 CUDA C++ 模板和抽象，用于在 CUDA 内核的所有级别和规模上实现高性能 GEMM 计算。与其他用于稠密线性代数的模板化 GPU 库（例如 MAGMA 库⁴）不同，CUTLASS 的目的是将 GEMM 的“活动部分”分解为由 C++ 模板类抽象的基本组件，从而允许程序员在自己的 CUDA 内核中轻松地自定义和专门化它们。我们正在 GitHub 上发布我们的 CUTLASS 源代码，作为 CUDA GEMM 技术的初始说明，这些技术将演变为模板库 API。

我们的 CUTLASS 原语包括对混合精度计算的广泛支持，为处理 8 位整数、半精度浮点数 (FP16)、单精度浮点数 (FP32) 和双精度浮点数 (FP64) 类型提供了专门的数据移动和乘累加抽象。CUTLASS 最令人兴奋的功能之一是使用 WMMA API 在 Volta 架构中的新 Tensor Core 上运行的矩阵乘法实现。Tesla V100 的 Tensor Core 是可编程的矩阵乘法累加单元，可以高效提供高达 125 Tensor TFLOP/s 的性能。

GPU 上的高效矩阵乘法

GEMM 计算 C = alpha A * B + beta C，其中 A、B 和 C 是矩阵。A 是 M 行 K 列的矩阵，B 是 K 行 N 列的矩阵，C 是 M 行 N 列的矩阵。为简单起见，让我们在以下示例中假设标量 alpha=beta=1。稍后，我们将展示如何使用支持任意缩放函数的 CUTLASS 实现自定义逐元素运算。

最简单的实现包含三个嵌套循环：

  
for (int i = 0; i < M; ++i)
    for (int j = 0; j < N; ++j)
       for (int k = 0; k < K; ++k) 
            C[i][j] += A[i][k] * B[k][j];

C 中位置 (i, j) 的元素是 A 的第 i 行和 B 的第 j 列的 K 元素点积。理想情况下，性能应受限于处理器的算术吞吐量。事实上，对于 M=N=K 的大规模方阵，矩阵乘积中的数学运算次数为 O(N3)，而所需数据量为 O(N2)，从而产生大约为 N 的计算强度。然而，利用理论计算强度需要重复使用每个元素 O(N) 次。不幸的是，上述“内积”算法依赖于在快速片上高速缓存中保存一个大型工作集，这会导致 M、N 和 K 增大时发生抖动。

一种更好的公式通过将 K 维数的循环架构为最外层循环来排列循环嵌套。这种计算形式加载 A 的一列和 B 的一行一次，计算其点积，并将此点积的结果累积到矩阵 C 中。在此之后，A 的这一列和 B 的这一行将不再被使用。

  
for (int k = 0; k < K; ++k)     // K dimension now outer-most loop
    for (int i = 0; i < M; ++i)
        for (int j = 0; j < N; ++j)
            C[i][j] += A[i][k] * B[k][j];

对于这种方法的一个担忧是它要求 C 的所有 M x N 元素都是活动的，以便存储每次乘加指令的结果，理想情况下在内存中可以写入的速度与乘加指令的计算速度一样快。我们可以通过将 C 分区为大小为 Mtile x Ntile 的切片，以减小 C 的工作集大小，这些切片可以保证放入片上内存。然后我们将“外部乘积”公式应用于每个切片。这导致了以下循环：

  
for (int m = 0; m < M; m += Mtile)                // iterate over M dimension
    for (int n = 0; n < N; n += Ntile)            // iterate over N dimension
        for (int k = 0; k < K; ++k)
            for (int i = 0; i < Mtile; ++i)       // compute one tile 
                for (int j = 0; j < Ntile; ++j) {
                    int row = m + i;
                    int col = n + j;
                    C[row][col] += A[row][k] * B[k][col];
                }

对于 C 的每个图块，A 和 B 的图块被精确地获取一次，从而实现了 O(N) 计算强度。C 的每个图块的大小可以选择为匹配目标处理器的 L1 缓存或寄存器的容量，并且嵌套的最外层循环可以轻松地并行化。这是一个巨大的进步！

进一步的重构提供了额外的机会来利用局部性和并行性。与其专门累积向量外积，我们可以通过分块遍历 K 维度来累积矩阵的乘积。我们通常将此概念称为累积矩阵乘积。

分层 GEMM 结构

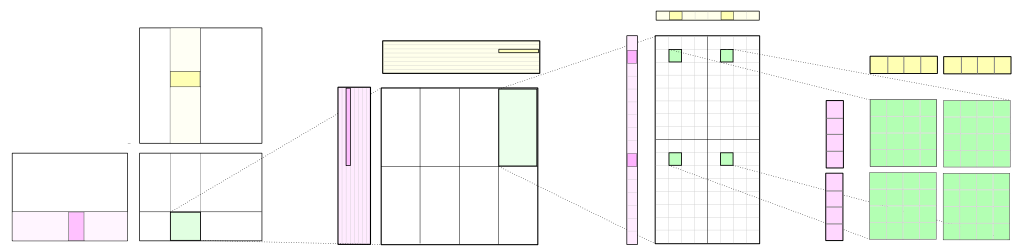
CUTLASS 通过将计算分解为线程块切片、经线切片和线程切片的层次结构，并应用累积矩阵乘积的策略，将切片结构应用于高效地为 GPU 实现 GEMM。此层次结构与 NVIDIA CUDA 编程模型非常相似，如图 1 所示。在此，您可以看到数据从全局内存移动到共享内存（矩阵到线程块切片）、从共享内存移动到寄存器文件（线程块切片到经线切片），以及从寄存器文件移动到 CUDA 核心进行计算（经线切片到线程切片）。

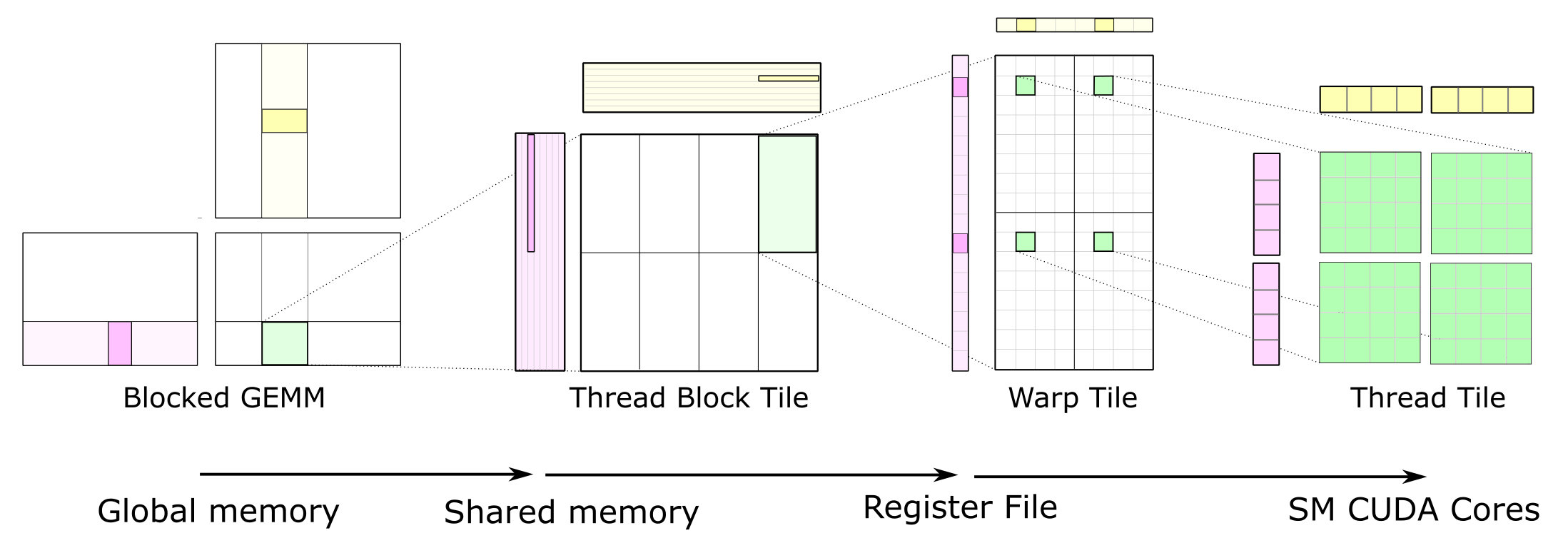图 1. 完整的GEMM层次结构将数据从较慢的内存传输到较快的内存，在较快的内存中，数据在许多数学运算中被重复使用。

Thread Block Tile 线程块切片

每个线程块通过迭代加载输入矩阵中的矩阵数据块并计算累积矩阵乘积 (C += A * B) 来计算其输出 GEMM 的部分。图 2 显示了单个线程块执行的计算，并突出了其主循环一次迭代中使用的数据块。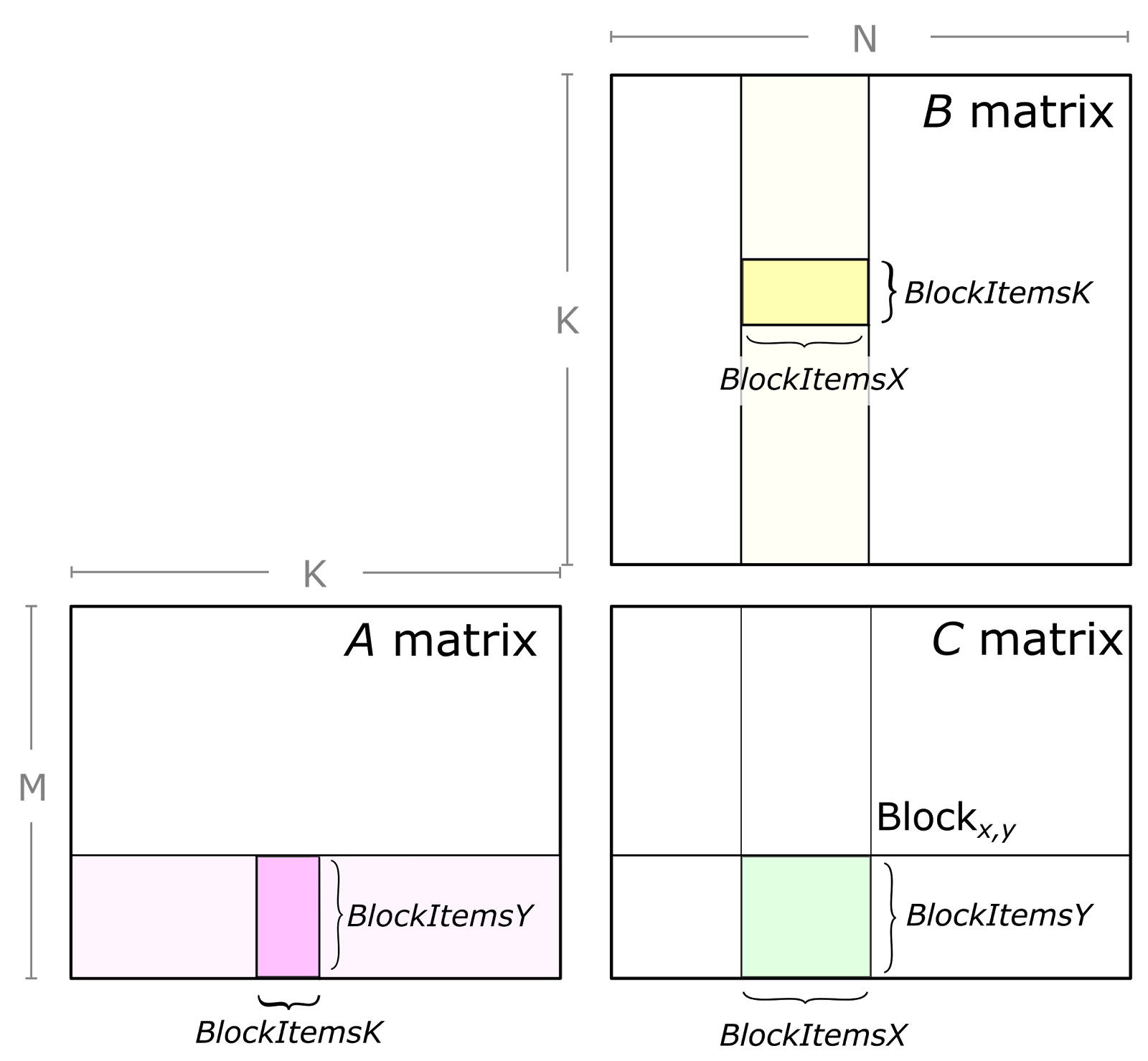图 2. 将 GEMM 问题分解为由单个线程块执行的计算。绿色显示的 C 子矩阵由 A 块和 B 子矩阵的矩阵乘法计算。这是通过循环遍历 K 维（已划分为块）并累加每个块的矩阵乘积结果来执行的。

CUDA 线程块图块结构进一步划分为 warp（以 SIMT 方式一起执行的线程组）。Warp 为 GEMM 计算提供了有用的组织，并且是 WMMA API 的显式部分，我们稍后将讨论。

图 3 显示了一个块级矩阵乘积结构的详细视图。从全局内存加载 A 和 B 的切片，并将其存储到所有 warp 都可访问的共享内存中。线程块的输出切片在空间上跨 warp 分区，如图 3 所示。我们将此输出切片的存储称为累加器，因为它存储累积矩阵乘积的结果。每个累加器在每次数学运算中更新一次，因此它需要驻留在 SM 中最快的内存：寄存器文件中。

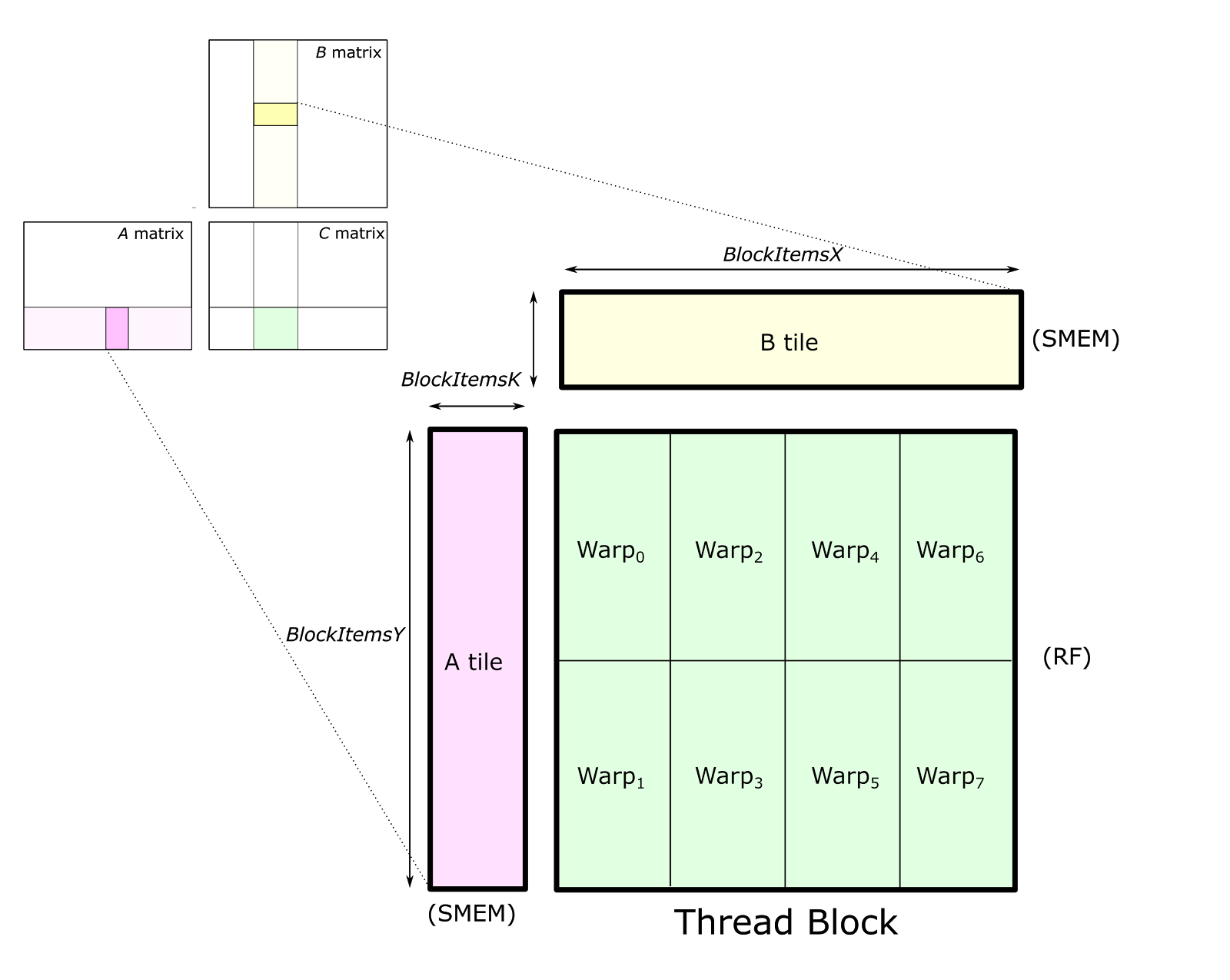图 3. 线程块结构将 C 的切片划分为多个 warp，每个 warp 存储一个不重叠的 2D 切片。每个 warp 将其累加器元素存储在寄存器中。A 和 B 的切片存储在所有线程块中的 warp 都可访问的共享内存中。

参数 BlockItems{X,Y,K} 是编译时常量，程序员指定这些常量以针对目标处理器和特定 GEMM 配置的长宽比（例如 M、N、K、数据类型等）调整 GEMM 计算。在图中，我们展示了一个八 warp、256 线程线程块，这对于 CUTLASS 中实现的大型 SGEMM（FP32 GEMM）切片大小来说是典型的。

Warp Tile Warp 切片

一旦数据存储在共享内存中，每个 warp 通过迭代线程块切片的 K 维度、从共享内存加载子矩阵（或片段）并计算累积外积来计算累积矩阵乘积序列。图 4 显示了详细视图。片段的大小通常在 K 维度中非常小，以最大化相对于从共享内存加载的数据量的计算强度，从而避免共享内存带宽成为瓶颈。 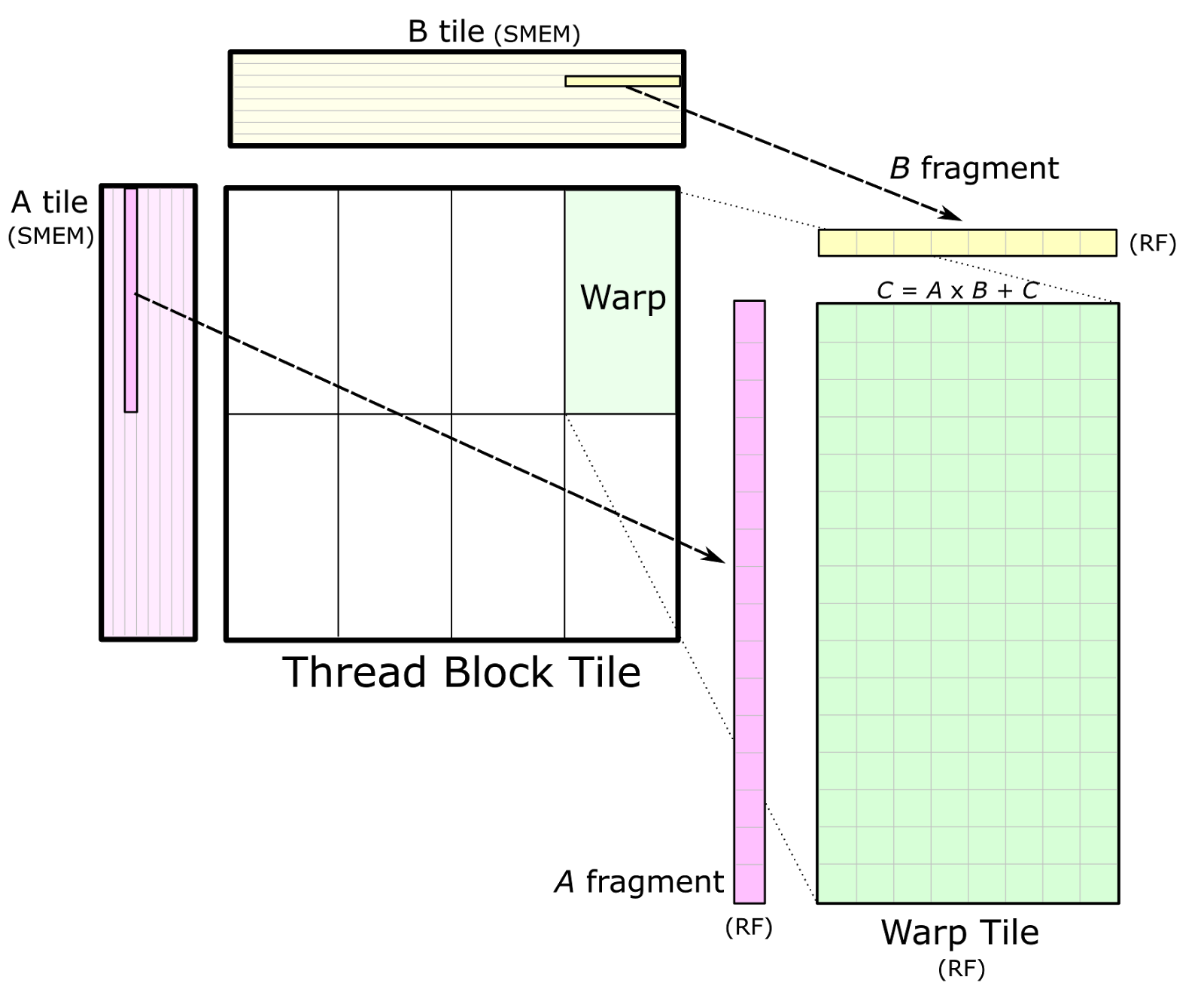图 4. 一个单独的 warp 通过迭代地将 A 和 B 的片段从相应的共享内存 (SMEM) 块加载到寄存器 (RF) 中并计算外部积来计算累积矩阵积

图 4 还描述了几个 warp 之间共享内存中的数据共享。线程块同一行中的 warp 加载 A 的相同片段，同一列中的 warp 加载 B 的相同片段。

我们注意到，GEMM 结构以 warp 为中心的组织在实现高效的 GEMM 内核方面是有效的，但并不依赖于隐式 warp 同步执行来实现同步。CUTLASS GEMM 内核与对 __syncthreads() 的调用很好地同步，具体取决于情况。

Thread Tile 线程图块

CUDA 编程模型根据线程块和各个线程进行定义。因此，warp 结构映射到各个线程执行的操作上。线程无法访问彼此的寄存器，因此我们必须选择一种组织方式，使寄存器中保存的值能够被同一线程执行的多个数学指令重复使用。这导致线程内出现 2D 平铺结构，如图 5 中的详细视图所示。每个线程向 CUDA 核心发出一个独立的数学指令序列，并计算累积的外积。

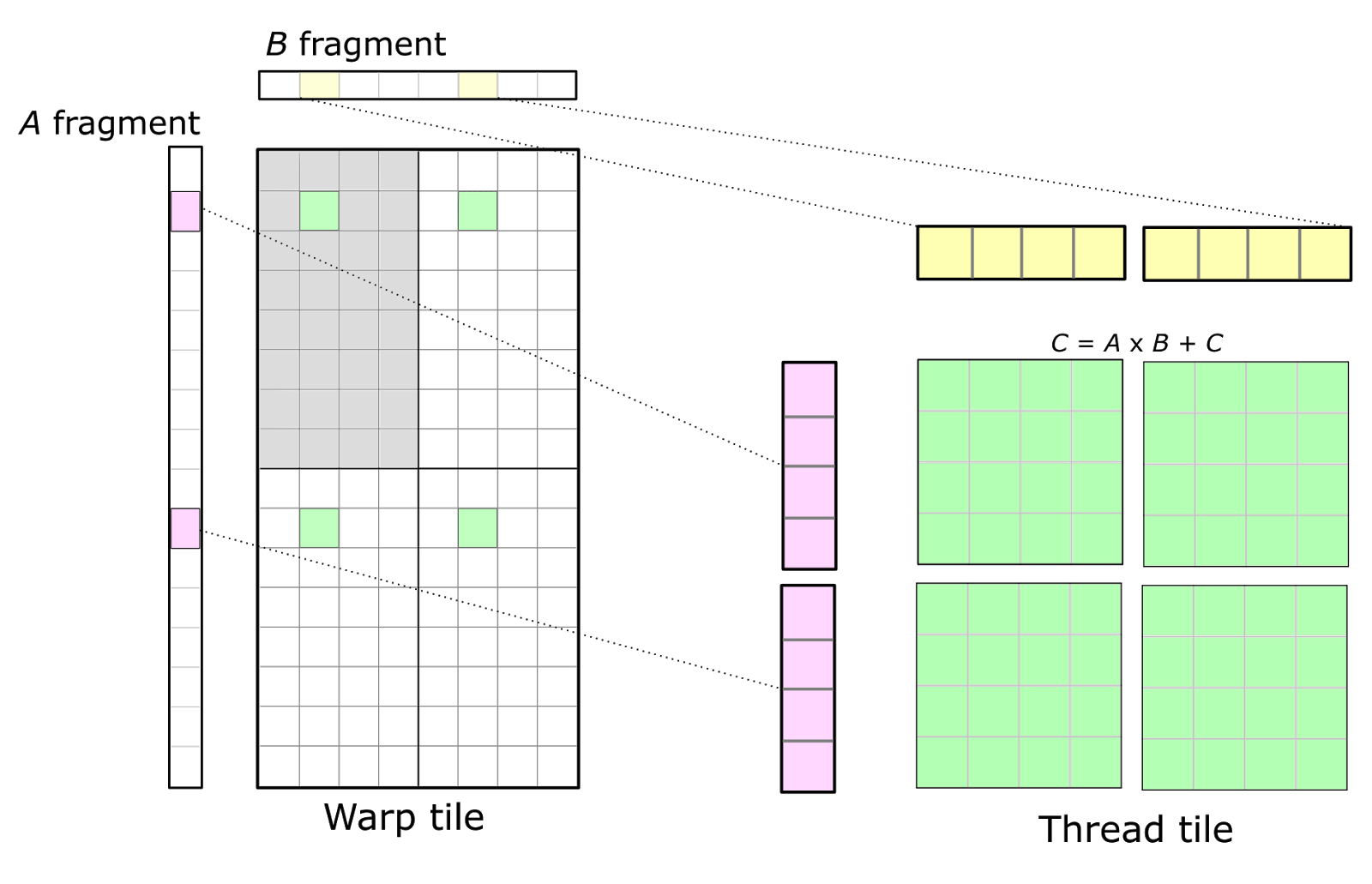图 5. 单个线程（右）通过计算寄存器中保存的 A 片段和 B 片段的外积，参与经线级矩阵乘法（左）。经线的累加器以绿色显示，在经线内的线程之间进行分区，通常排列为一组 2D 平铺。

在图 5 中，经线的左上角象限以灰色阴影显示。32 个单元格对应于经线内的 32 个线程。这种排列导致同一行或同一列中的多个线程分别获取 A 和 B 片段的相同元素。为了最大化计算强度，可以复制此基本结构以形成完整的经线级累加器平铺，从而产生由 8x1 和 1x8 片段的外积计算得出的 8x8 整体线程平铺。这由绿色显示的四个累加器平铺来说明。

WMMA GEMM

经线平铺结构可以使用 CUDA 9 中引入的 CUDA Warp 矩阵乘累加 API (WMMA) 来实现，以针对 Volta V100 GPU 的 Tensor Core。有关 WMMA API 的更多详细信息，请参阅博文在 CUDA 9 中编程 Tensor Core。

每个张量核心提供一个 4x4x4 矩阵处理阵列，执行操作 D = A * B + C，其中 A、B、C 和 D 是 4×4 矩阵，如图 6 所示。矩阵乘法输入 A 和 B 是 FP16 矩阵，而累加矩阵 C 和 D 可以是 FP16 或 FP32 矩阵。

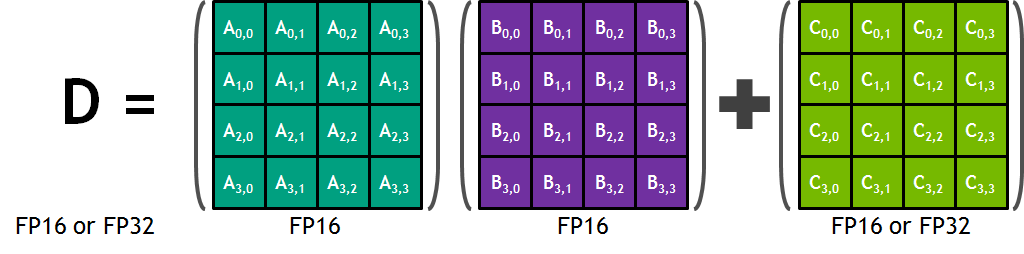图 6. WMMA 计算 D = A * B + C，其中 A、B、C 和 D 是矩阵。

实际上，WMMA API 是上一节中描述的线程切片结构的替代方案，用于经线范围的矩阵乘法累加操作。WMMA API 不会将经线切片结构分解为由各个线程拥有的标量和向量元素，而是为程序员提供经线协作矩阵片段加载/存储和乘法累加数学运算的抽象。

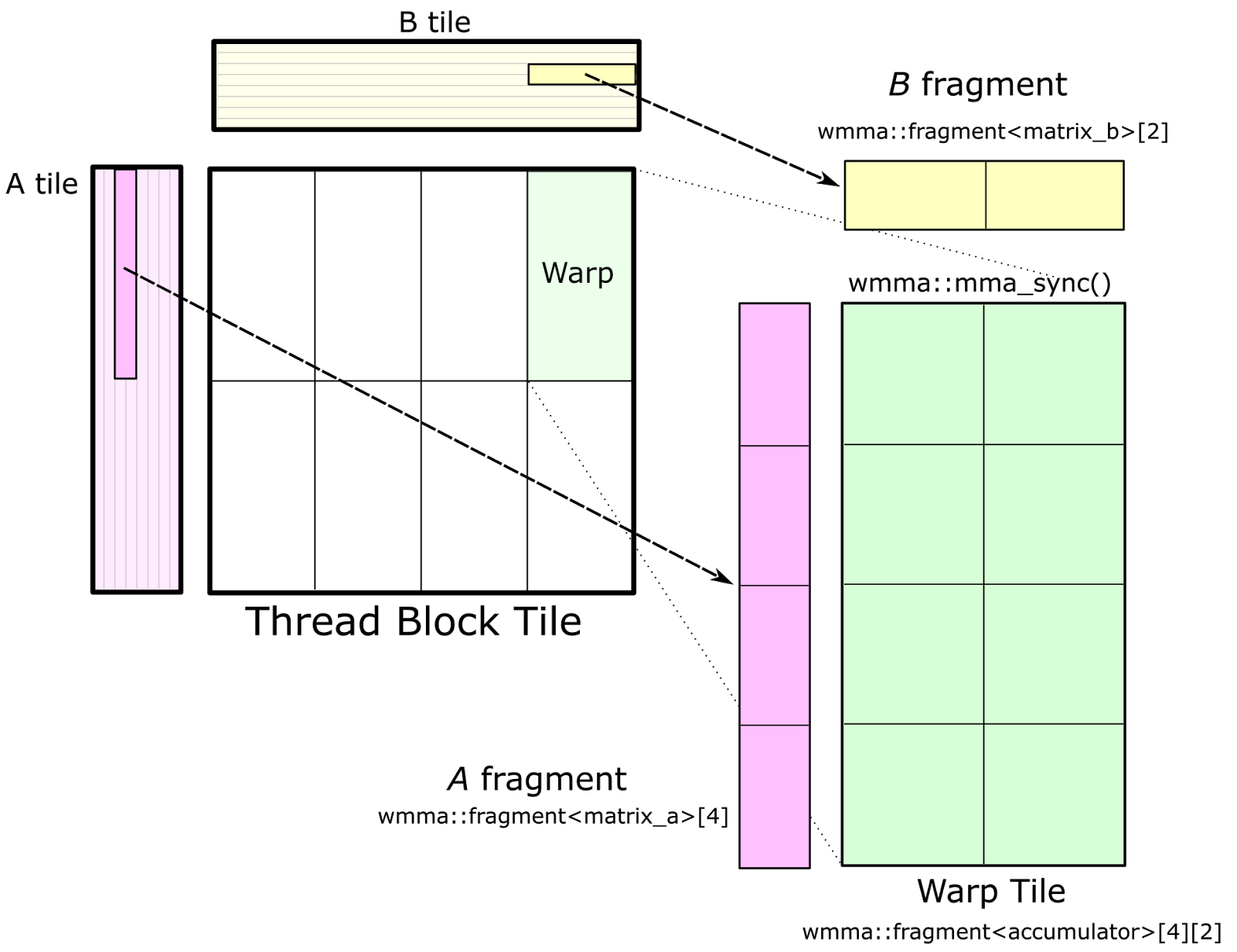
图 7 展示了针对 CUDA WMMA API 的经纬度瓦片结构。对 wmma::load_matrix_sync 的调用将 A 和 B 的片段加载到 nvcuda::wmma::fragment<> 模板的实例中，经纬度瓦片的累加器元素被构造为nvcuda::wmma::fragment<accumulator> 对象的数组。这些片段存储了分布在经纬度线程中的 2D 矩阵。最后，对每个累加器片段（以及 A 和 B 中的对应片段）的 nvcuda::wmma::mma_sync() 调用使用张量核计算经纬度范围的矩阵乘法累加操作。

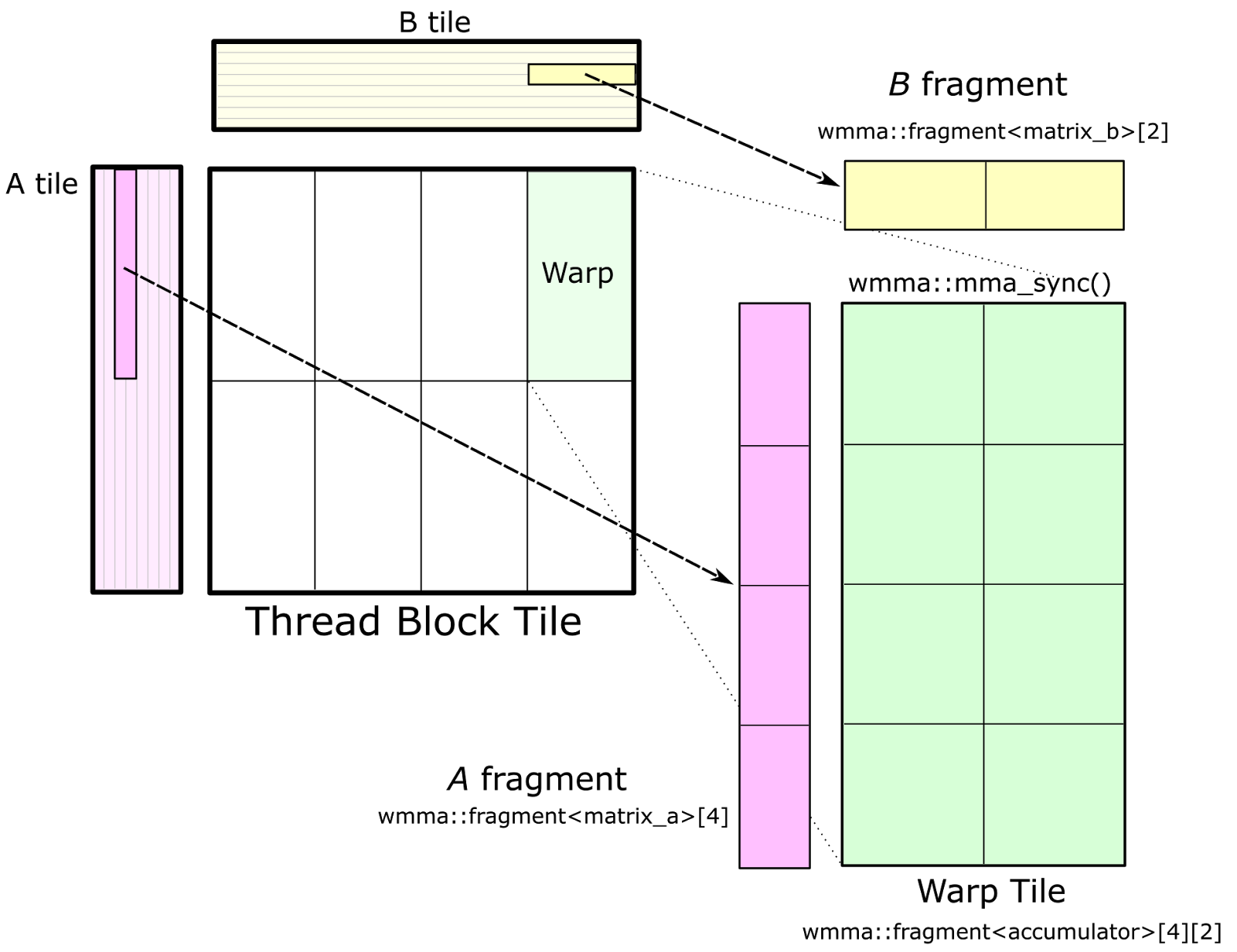图 7. 可以使用 CUDA WMMA API 实现经纱瓦片结构，以针对 Volta V100 的 Tensor Core。此 API 提供了用于加载矩阵片段和执行矩阵乘法累加的抽象。

CUTLASS 在文件 block_task_wmma.h 中实现了基于 WMMA API 的 GEMM。经纱平铺必须具有维度，这些维度是目标 CUDA 计算能力的 nvcuda::wmma 模板定义的矩阵乘法累加形状的倍数。在 CUDA 9.0 中，基本 WMMA 大小为 16x16x16。

完整的 GEMM

完整的 GEMM 结构可以表示为由线程块的线程执行的嵌套循环，如下面的清单所示。除了最外层的“main”循环之外，所有循环都具有恒定的迭代次数，并且可以由编译器完全展开。为了简洁起见，这里省略了地址和索引计算，但在 CUTLASS 源代码中进行了说明。

  
// Device function to compute a thread block’s accumulated matrix product
__device__ void block_matrix_product(int K_dim) {
    
    // Fragments used to store data fetched from SMEM
    value_t frag_a[ThreadItemsY];
    value_t frag_b[ThreadItemsX];

    // Accumulator storage
    accum_t accumulator[ThreadItemsX][ThreadItemsY];

    // GEMM Mainloop - iterates over the entire K dimension - not unrolled
    for (int kblock = 0; kblock < K_dim; kblock += BlockItemsK) {

        // Load A and B tiles from global memory and store to SMEM
        //
        // (not shown for brevity - see the CUTLASS source for more detail)
        ...

        __syncthreads();
        
        // Warp tile structure - iterates over the Thread Block tile
        #pragma unroll
        for (int warp_k = 0; warp_k < BlockItemsK; warp_k += WarpItemsK) {

            // Fetch frag_a and frag_b from SMEM corresponding to k-index 
            //
            // (not shown for brevity - see CUTLASS source for more detail)
            ...

            // Thread tile structure - accumulate an outer product
            #pragma unroll
            for (int thread_x = 0; thread_x < ThreadItemsX; ++thread_x) {
                #pragma unroll
                for (int thread_y=0; thread_y < ThreadItemsY; ++thread_y) {
                    accumulator[thread_x][thread_y] += frag_a[y]*frag_b[x];
                }
            }
        }

        __syncthreads();
    }   
}

WarpItemsK 指目标数学运算的点积大小。对于 SGEMM（FP32 GEMM）、DGEMM（FP64）和 HGEMM（FP16），标量乘累加指令的点积长度为 1。对于 IGEMM（8 位整数 GEMM），CUTLASS 以四元素整数点积指令 (IDP4A) 为目标，其中 WarpItemsK=4 。对于基于 WMMA 的 GEMM，我们选择 wmma::fragment<> 模板的 K 维。目前，这被定义为 WarpItemsK=16 。

软件流水线

平铺矩阵乘法广泛使用寄存器文件来保存片段和累加器平铺以及大共享内存分配。片上存储的相对较高需求限制了占用率，即一个 SM 上可以同时运行的最大线程块数。因此，GEMM 实现可以在每个 SM 中容纳的波束和线程块远少于 GPU 计算工作负载的典型情况。我们使用软件流水线通过在循环中同时执行 GEMM 层次结构的所有阶段并在此后迭代期间将每个阶段的输出馈送到其相关阶段来隐藏数据移动延迟，如图 8 所示。

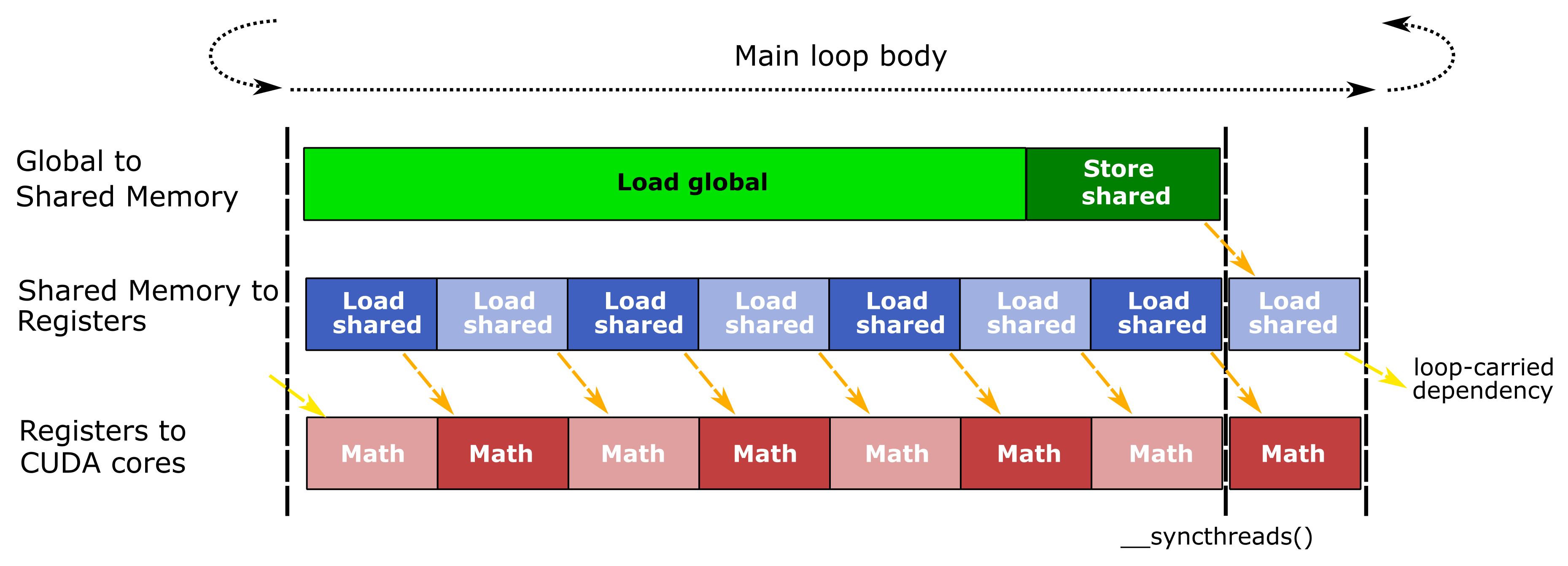图 8. CUTLASS GEMM 实现的主循环中交错的三条并发指令流。橙色箭头显示数据依赖性。当内存系统从全局内存加载数据，SM 为下一个线程块加载片段时，线程通过执行当前块的数学指令使 SM 保持忙碌状态。

GEMM CUDA 内核在管道内发出三个并发操作流，它们对应于 GEMM 层次结构内数据流的阶段（图 1）。图中每个阶段的相对大小指示操作的延迟是长还是短，橙色箭头突出显示了每个流的阶段之间的数据依赖性。在将数据存储到共享内存后调用 __syncthreads() 会同步所有波束，以便它们可以在没有竞争条件的情况下读取共享内存。管道的最终数学阶段与从共享内存加载重叠，该加载将数据馈送到下一个主循环迭代的第一个数学阶段。

实际上，CUDA 程序员通过在程序文本中交错每个阶段的 CUDA 语句，并依靠 CUDA 编译器在编译代码中发出适当的指令计划，在管道阶段之间实现指令级并发。广泛使用 #pragma unroll和编译时常量使 CUDA 编译器能够展开循环并将数组元素映射到寄存器，这两者对于可调优的高效实现都至关重要。请参阅 block_task::consume_tile() 以获取示例。

我们在 GEMM 层次的每个级别使用双缓冲，以使上游管道阶段能够将数据写入共享内存或寄存器，而从属管道阶段从其存储元素加载数据。值得注意的是，这消除了第二个 __syncthreads()，因为一个共享内存缓冲区在写入时另一个正在读取。双缓冲的成本是共享内存容量的两倍，并且用于保存共享内存获取的寄存器数量的两倍。

实际可用的延迟隐藏量取决于线程块、warp 和线程切片的尺寸，以及 SM 内活动数学功能单元的吞吐量。虽然较大的切片为数据重用提供了更多机会，并且可能提供更多的延迟隐藏，但 SM 寄存器文件和共享内存的物理容量限制了最大切片大小。幸运的是，NVIDIA GPU 拥有足够的存储资源来执行足够大的 GEMM 切片，以受到数学限制！

CUTLASS

CUTLASS 是分层 GEMM 结构的实现，作为 CUDA C++ 模板类。我们打算将这些模板包含在现有的设备端 CUDA 内核和函数中，但我们还提供了一个示例内核和启动接口，以便快速启动和运行。与 CUB 一样，广泛使用模板参数和编译时常量使 CUTLASS 具有可调性和灵活性。

CUTLASS 为高效 GEMM 实现所需的运算实现了抽象。专门的“tile 加载器”将数据从全局内存高效地移动到共享内存中，适应源数据的布局，同时还能高效、无冲突地加载到寄存器中。对于某些布局，IGEMM 需要对数据进行一些重组以针对 CUDA 的 4元素整数点积指令，并且在将数据存储到 SMEM 时会执行此操作。

CUTLASS GEMM 设备函数

以下来自 dispatch.h 的示例定义了一个 block_task 类型，并实例化了一个 GEMM，用于假设列主序输入矩阵的浮点数据。 block_task_policy_t 定义了 GEMM tile 大小，并在下一部分中进行了详细讨论。

  
/// CUTLASS SGEMM example
__global__ void gemm_kernel(
    float *C, 
    float const *A, 
    float const *B, 
    int M, 
    int N, 
    int K) {

    // Define the GEMM tile sizes - discussed in next section
    typedef block_task_policy <
        128, // BlockItemsY: Height in rows of a tile
        32, // BlockItemsX - Width in columns of a tile
        8, // ThreadItemsY - Height in rows of a thread-tile
        4, // ThreadItemsX - Width in columns of a thread-tile
        8, // BlockItemsK - Depth of a tile
        true, // UseDoubleScratchTiles - whether to double-buffer SMEM
        block_raster_enum::Default // Block rasterization strategy
    > block_task_policy_t;

    // Define the epilogue functor
    typedef gemm::blas_scaled_epilogue<float, float, float> epilogue_op_t ;

    // Define the block_task type.
    typedef block_task < 
        block_task_policy_t, 
        float, 
        float, 
        matrix_transform_t::NonTranspose, 
        4, 
        matrix_transform_t::NonTranspose, 
        4, 
        epilogue_op_t, 
        4, 
        true 
    > block_task_t;

    // Declare statically-allocated shared storage
    __shared__ block_task_t::scratch_storage_t smem;

    // Construct and run the task
    block_task_t(
        reinterpret_cast(&smem),
        &smem,
        A,
        B,
        C,
        epilogue_op_t(1, 0),
        M,
        N,
        K).run();
}

共享内存分配 smem 由 block_task_t 实例用于在矩阵乘法计算中存储线程块级别的图块。

epilogue_op_t 是一个模板参数，它指定了一个函数对象，该函数对象用于在矩阵乘法操作完成后更新输出矩阵。这使您可以轻松地将矩阵乘法与自定义逐元素操作组合起来，正如我们在后面更详细地描述的那样。CUTLASS 提供了 gemm::blas_scaled_epilogue 函数对象实现来计算熟悉的 GEMM 操作 C = alpha * AB + beta * C（在 epilogue_function.h 中定义）。

CUTLASS GEMM 策略

CUTLASS 将指定 GEMM 层次结构中每个级别的 tile 大小的编译时常量组织为 gemm::block_task_policy 模板的专业化，该模板具有以下声明。

  
template <
    int BlockItemsY,            /// Height in rows of a tile in matrix C
    int BlockItemsX,            /// Width in columns of a tile in matrix C
    int ThreadItemsY,           /// Height in rows of a thread-tile in C
    int ThreadItemsX,           /// Width in columns of a thread-tile in C
    int BlockItemsK,            /// Number of K-split subgroups in a block
    bool UseDoubleScratchTiles, /// Whether to double buffer shared memory 
    grid_raster_strategy::kind_t RasterStrategy  /// Grid <a href="https://developer.nvidia.com/discover/ray-tracing">rasterization</a> strategy
> struct block_task_policy;

线程块碎片的大小分别为 ```ThreadItemsY-by-1和ThreadItemsX-by-1``。在上述示例中，它们分别表示来自 A 的 8-by-1 向量和来自 B 的 4-by-1 向量。

定义了策略类型后，我们可以定义 gemm::block_task 的类型，即 CUTLASS GEMM。此模板具有以下参数列表。

  
template <
    /// Parameterization of block_task_policy
    typename block_task_policy_t,

    /// Multiplicand value type (matrices A and B)
    typename value_t,
    /// Accumulator value type (matrix C and scalars)
    typename accum_t,

    /// Layout enumerant for matrix A
    matrix_transform_t::kind_t  TransformA,
    
    /// Alignment (in bytes) for A operand
    int LdgAlignA,
 
    /// Layout enumerant for matrix B
    matrix_transform_t::kind_t  TransformB,

    /// Alignment (in bytes) for B operand
    int LdgAlignB,

    /// Epilogue functor applied to matrix product
    typename epilogue_op_t,

    /// Alignment (in bytes) for C operand
    int LdgAlignC,

    /// Whether GEMM supports matrix sizes other than mult of BlockItems{XY}
    bool Ragged              
> struct block_task;

value_t 和 accum_t 分别指定源操作数和累加器矩阵的类型。 TransformA 和 TransformB 分别指定操作数 A 和 B 的布局。尽管我们尚未详细讨论矩阵布局，但 CUTLASS 支持行优先和列优先输入矩阵的所有组合。

LdgAlignA 和 LdgAlignB 指定保证对齐，这使得 CUTLASS 设备代码能够使用矢量内存操作。例如，8 字节的对齐允许 CUTLASS 在双元素矢量中加载类型 float 的元素。这通过减少 GPU 内正在进行的内存操作数量来减小代码大小并提高性能。更重要的是， ragged 处理指示矩阵维度是否可以是任意大小（满足对齐保证）。如果此模板参数为 false，则矩阵 A、B 和 C 预期都具有维度，这些维度是 block_task_policy 中的平铺参数的倍数。

将逐元素运算与 SGEMM 融合

深度学习计算通常在 GEMM 计算后执行简单的逐元素操作，例如计算激活函数。这些带宽受限层可以融合到 GEMM 操作的末尾，以消除额外的内核启动并避免通过全局内存进行往返。

以下示例演示了 GEMM 模板的一个简单应用，该模板向缩放矩阵乘积添加偏差项，然后应用 ReLU 函数将结果限制为非负值。通过将尾声分离到一个函子中，传递诸如指向其他矩阵和张量参数或其他比例因子的参数变得简单，并且不会妨碍 GEMM 实现。

首先，我们定义一个实现 gemm::epilogue_op 概念的类。构造函数和其他方法在此处未显示，但元素级偏差和 ReLU 操作显示在函数调用运算符的实现中。

  
template <typename accum_t, typename scalar_t, typename output_t>
struct fused_bias_relu_epilogue {

    // Data members pass additional arguments to epilogue
    scalar_t const *Bias;
    accum_t threshold;

    /// Constructor callable on host and device initializes data members
    inline __device__ __host__
    fused_bias_relu_epilogue(
        scalar_t const *Bias,
        accum_t threshold
    ): Bias(Bias), threshold(threshold) { }

    /// Applies bias + ReLu operation
    inline __device__ __host__
    output_t operator()(
        accum_t accumulator,  /// element of matrix product result
        output_t c,           /// element of source accumulator matrix C
        size_t idx            /// index of c element; may be used to load
                              /// elements from other identically-
                              /// structured matrices
        ) const {

        // Compute the result by scaling the matrix product, adding bias, 
        // and adding the scaled accumulator element.

        accum_t result = output_t(
            alpha * scalar_t(accumulator) +
            Bias[i] +                         // load and add the bias
            beta * scalar_t(c)
        );

        // apply clamping function
        return max(threshold, result);
    }
};

接着我们把该操作符作为结尾操作。

  
// New: define type for custom epilogue functor
typedef fused_bias_relu_epilogue_t<float, float, float> 
    bias_relu_epilogue_t;

/// Computes GEMM fused with Bias and ReLu operation
__global__ void gemm_bias_relu(
    ...,                                    /// GEMM parameters not shown 
    bias_relu_epilogue_t bias_relu_op) {    /// bias_relu_op constructed 
                                            /// by caller

    // Define the block_task type.
    typedef block_task<
        block_task_policy_t,          // same policy as previous example
        float,
        float,
        matrix_transform_t::NonTranspose,
        4,
        matrix_transform_t::NonTranspose,
        4,
        bias_relu_epilogue_t,         // New: custom epilogue functor type
        4,
        true
    > block_task_t ;

    // Declare statically-allocated shared storage
    __shared__ block_task_t::scratch_storage_t smem;
    
    // Construct and run the task
    block_task_t(
        reinterpret_cast(&smem),
        &smem,
        A,
        B,
        C,
        bias_relu_op,                 // New: custom epilogue object
        M,
        N,
        K).run();
}

这个简单的例子展示了将通用编程技术与高效的 GEMM 实现相结合的价值。

Tesla V100 (Volta) 性能

CUTLASS 非常高效，其性能与用于标量 GEMM 计算的 cuBLAS 相当。图 9 显示了 CUTLASS 相对于使用 CUDA 9.0 编译的 cuBLAS 在 NVIDIA Tesla V100 GPU 上运行的性能，用于大矩阵维度 (M=10240, N=K=4096)。图 9 显示了 CUTLASS 支持的每种计算数据类型的相对性能，以及输入操作数的所有行优先和列优先布局排列。

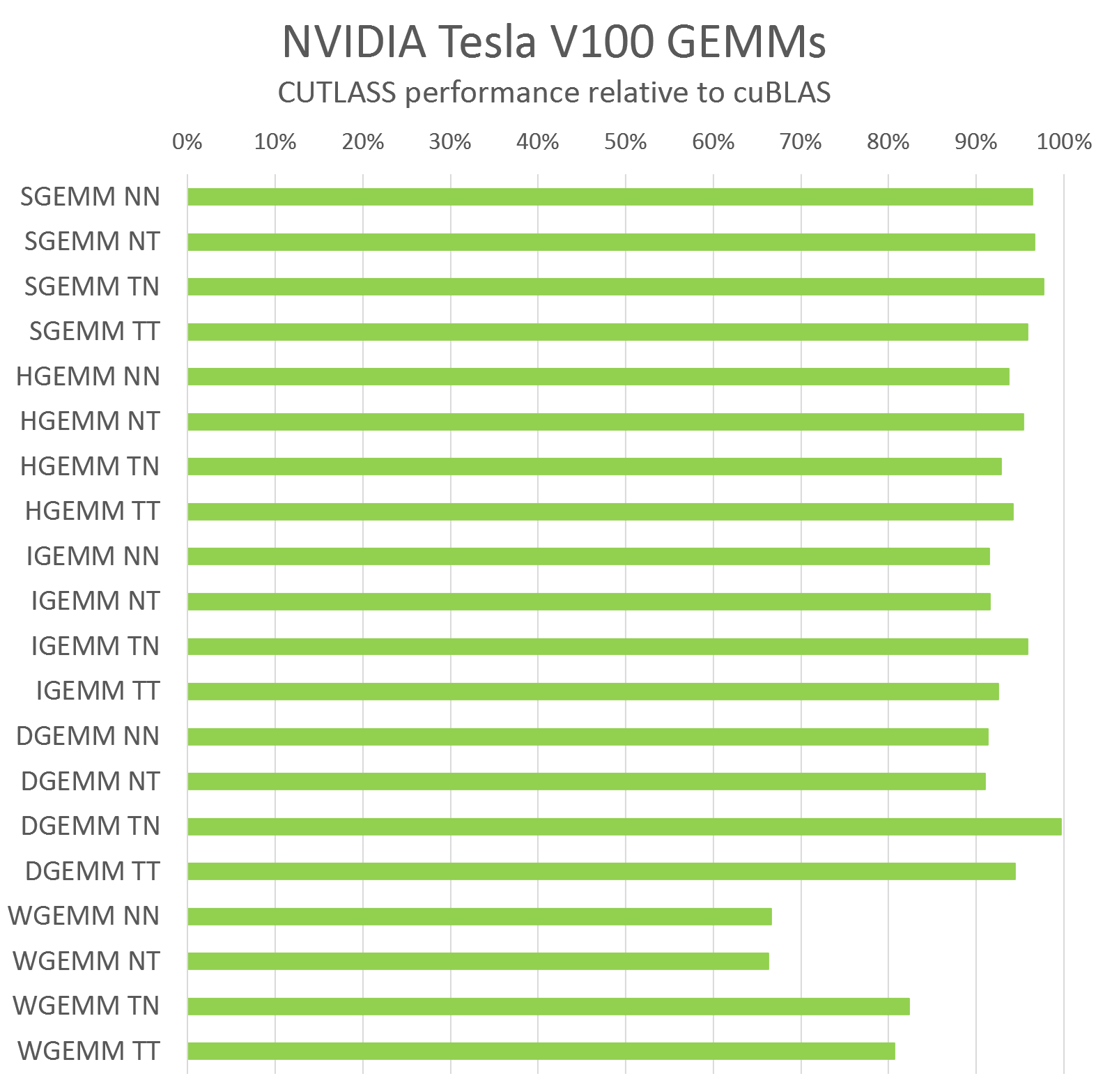图 9. 相对于为每种 GEMM 数据类型和矩阵布局编译的 cuBLAS，CUTLASS 的相对表现力。按照 BLAS 惯例，矩阵通常按列为主，除非转置。也就是说，“N”表示按列为主的矩阵，“T”表示按行为主的矩阵。

在大多数情况下，CUTLASS C++ 与 cuBLAS 手工调整的汇编内核的性能相差不到几个百分点。对于 WMMA GEMM（图 9 中的 WGEMM 运算），CUTLASS 尚未达到与 cuBLAS 相同的性能，但我们正与 CUDA 编译器和 GPU 架构团队紧密合作，以开发技术在 CUDA 代码中达到类似的性能水平。

尝试cutlass

文中我们没有讨论很多有趣的细节，所以我们建议你去了解 CUTLASS 储存库并亲自尝试 CUTLASS。cutlass_test 样本程序演示了如何调用 CUTLASS GEMM 内核（一种用于矩阵乘法的优化内核），验证其计算结果，并评估其性能。我们期待你的反馈，也欢迎在评论区留下你的意见或与我们取得联系！

Acknowledgements

特别感谢 Joel McCormack 提供的技术见解和解释，尤其是在 NVIDIA 微架构以及 cuBLAS 和 cuDNN 使用的技术方面.

Reference

Sharan Chetlur, Cliff Woolley, Philippe Vandermersch, Jonathan Cohen, John Tran, Bryan Catanzaro, Evan Shelhamer. cuDNN: Efficient Primitives for Deep Learning, arXiv:1410.0759, 2014. ↩
Michael Mathieu, Mikael Henaff, Yann LeCun. Fast training of Convolutional Networks through FFTs. arXiv:1312.5851. 2013. ↩
Andrew Lavin, Scott Gray. Fast Algorithms for Convolutional Neural Networks. arXiv:1509.09308. 2015. ↩
MAGMA. http://icl.cs.utk.edu/magma/index.html ↩

CUDA, GEMM, CUTLASS

Translation

This post is licensed under CC BY 4.0 by the author.